
Robert Breedlove ![]()
The « What is Money? » show podcast
Parallax Digital
Page Medium de l’auteur
Satoshi a offert Bitcoin au monde, un véritable don gratuit. Sa découverte de la rareté absolue de la monnaie est une idée imparable qui bouleverse le monde, à l’instar de son ancêtre numérique, le chiffre zéro, à son époque.
Zéro est spécial
« Dans l'histoire de la culture, la découverte du chiffre zéro restera à jamais l'une des plus grandes percées de l'humanité. »
- Tobias Danzig, Number: The Language of Science
Nombreux sont ceux qui pensent que Bitcoin n’est « qu’une crypto-monnaie parmi des milliers d’autres », ce qui est aussi vrai que de considérer que zéro n’est qu’un chiffre parmi une série infinie de chiffres. En réalité, Bitcoin est spécial, tout comme le zéro : l’un et l’autre sont des inventions qui ont conduit à des découvertes qui ont fondamentalement remodelé la totalité de leur propre système : pour Bitcoin, ce système c’est la monnaie, et pour le chiffre zéro, il s’agit des mathématiques. La monnaie et les mathématiques étant les deux langages universels de l’humanité, Bitcoin et le chiffre zéro sont des constructions essentielles pour la civilisation.
Durant la plus grande partie de son histoire, l’humanité ne possédait aucune notion du zéro : la compréhension d’un tel concept ne nous est pas innée. Il a donc fallu inventer un symbole pour le représenter et l’enseigner sans relâche pour le transmettre de génération en génération. Le chiffre zéro est une notion abstraite qui n’est pas perceptible dans le monde physique : personne ne part acheter zéro pomme. Pour mieux comprendre tout cela, nous allons emprunter un chemin sinueux qui parcourt plus de 4000 ans de l’Histoire de l’humanité et qui a vu le chiffre zéro s’intégrer dans le socle empirique de la modernité.
Les chiffres, qui sont les symboles des nombres, sont les plus grandes abstractions jamais inventées par l’humanité : presque tout ce avec quoi nous interagissons est mieux appréhendé sous forme numérique, quantifiable. Les mathématiques, le langage des chiffres, trouvent leur origine dans le désir pratique de pouvoir compter les choses, qu’il s’agisse de la quantité de poissons pêchés chaque jour ou du nombre de jours écoulés depuis la dernière pleine lune. De nombreuses civilisations anciennes ont mis au point des systèmes de numération rudimentaires : en l’an 2000 avant notre ère, les Babyloniens, qui n’étaient pas parvenus à conceptualiser le zéro, employaient deux symboles qu’ils agençaient dans des configurations différentes pour créer des chiffres uniques compris entre 1 et 60 :

Le cunéiforme babylonien était un système de numération assez inefficace – notez combien de traits d’écriture sont nécessaires pour symboliser chaque nombre – et le calcul à l’aide de ce système était encore plus fastidieux.
Des vestiges du système cunéiforme babylonien en base 60 subsistent encore aujourd’hui : on compte 60 secondes dans une minute, 60 minutes dans une heure, et 6 séries de 60 degrés dans un cercle. Mais ce système ancien ne comportait pas de zéro, ce qui en limitait considérablement l’utilité. Les Grecs et les Mayas de l’Antiquité développèrent leurs propres systèmes de numération, qui contenaient chacun des conceptions approximatives du zéro. Cependant, la première utilisation explicite et arithmétique du zéro provient des anciennes cultures indienne et cambodgienne. Elles créèrent un système de neuf symboles numériques et d’un petit point utilisé pour marquer l’absence d’un nombre, le zéro originel. Ce système de numération a ensuite évolué pour devenir celui que nous utilisons aujourd’hui :

Le premier zéro écrit connu : tiré du manuscrit Bakhshali, dont certaines pages datent des IIIe et IVe siècles de notre ère.

L’inscription K-127 (N.d.T : gravée sur une stelle Khmer ancienne] porte le plus ancien zéro connu à ce jour – datée du 7e siècle, elle fut découverte au Cambodge au 19ème siècle.
Au VIIe siècle, le mathématicien indien Brahmagupta développe des termes pour le zéro dans l’addition, la soustraction, la multiplication et la division (bien qu’il rencontre quelques difficultés avec cette dernière opération, comme ce sera le cas pour les penseurs des siècles ultérieurs). À mesure que la discipline mathématique mûrit en Inde, elle est transmise par les réseaux commerciaux à l’est vers la Chine, et à l’ouest au cœur des cultures islamiques et arabes. C’est cette avancée occidentale du zéro qui a finalement conduit à la création du système de numération indo-arabe, le moyen de représentation symbolique des chiffres le plus répandu dans le monde aujourd’hui :
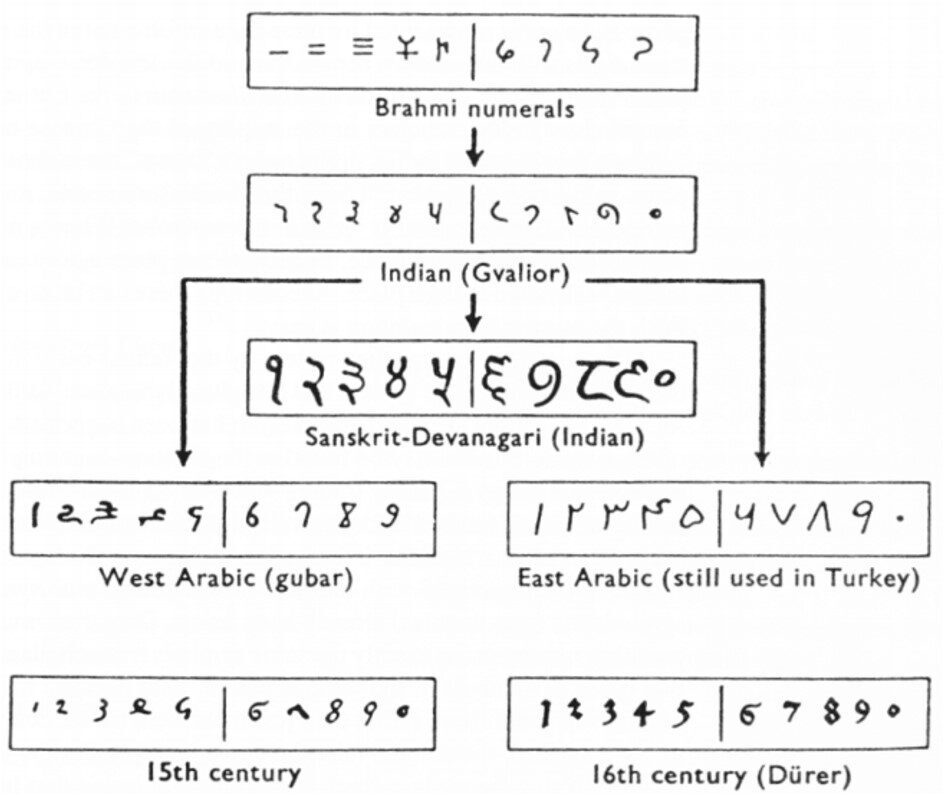
L'économicisation des mathématiques
Lorsque le chiffre zéro atteint l’Europe environ 300 ans plus tard, pendant le Haut Moyen Âge, il se heurte à une forte résistance idéologique. Face à l’opposition des utilisateurs du système numéral romain bien établi, le zéro peine à gagner du terrain en Europe. À l’époque, les gens peuvent se passer du zéro, mais ils sont à mille lieues de réaliser combien il est inefficace d’effectuer des calculs sans le zéro. Une analogie pertinente s’impose ici : tant les mathématiques que la monnaie sont possibles respectivement sans le zéro et Bitcoin, mais, privés de ces éléments fondamentaux, ces deux systèmes s’avèrent terriblement inefficients. Notez combien il est difficile de faire de l’arithmétique en chiffres romains :
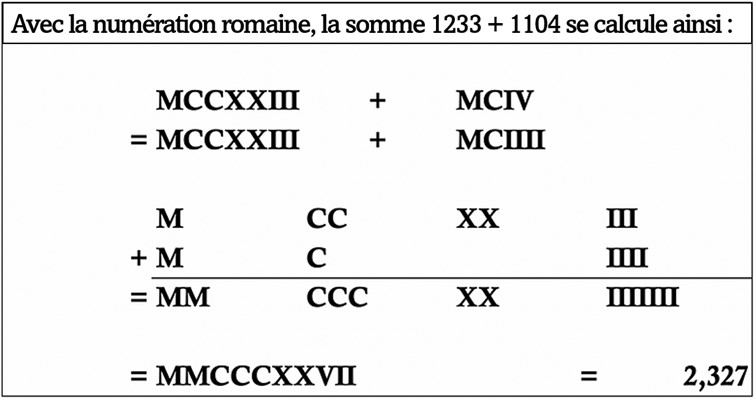
Si vous vous croyiez nul en arithmétique avec des chiffres, essayez donc de le faire avec des lettres.
Le système de numération indo-arabe permet des calculs nettement plus simples qu’avec la numération romaine, et les systèmes économes en énergie tendent à l’emporter sur le long terme, comme nous l’avons constaté lorsque la machine à vapeur a surclassé l’énergie d’origine animale ou lorsque le capitalisme l’a emporté sur le socialisme (autre point important à garder en mémoire pour plus tard concernant Bitcoin). L’exemple ci-dessus ne révèle que les difficultés associées à l’addition – la multiplication et la division étaient autrement plus laborieuses. Comme le décrit Amir D. Aczel dans son livre Finding Zero :
« Le système de numération indo-arabe a permis une immense économie d’écriture, étant donné que le même chiffre, par exemple 4, peut être utilisé pour se représenter lui-même ou quarante (40) lorsqu’il est suivi d’un zéro, ou quatre cent quatre lorsqu’il est écrit 404, ou quatre mille lorsqu’il est écrit sous la forme d’un 4 suivi de trois zéros (4 000). La puissance du système de numération indo-arabe est incomparable, car il représente les nombres de manière efficace et compacte, ce qui nous permet d’effectuer des calculs arithmétiques compliqués qui auraient été extrêmement difficiles auparavant. »
L’inefficacité de la numération romaine ne devait pas être tolérée beaucoup plus longtemps dans un monde qui s’enrichissait par le commerce. La prolifération des réseaux commerciaux et des gains de productivité incessants multipliaient les perspectives de création de richesses, qui incitaient les marchands à être toujours plus compétitifs, à rechercher constamment comment gagner un nouvel avantage sur les autres. Le calcul et la tenue de registres avec un système de numération basé sur le zéro étaient qualitativement plus faciles, quantitativement plus rapides et occasionnait moins d’erreurs. Malgré la résistance de l’Europe, ce nouveau système de numération ne pouvait tout simplement pas être ignoré : une telle situation était amenée à se représenter plus tard pour Bitcoin son lointain descendant. Le chiffre zéro était une idée imparable dont le temps était venu :

Fonctions du zéro
La première fonction du zéro est de servir de symbole dans notre système numérique : par exemple, remarquez le « 0 » dans le nombre « 1 104 » de l’équation ci-dessus : il indique l’absence de valeur dans la dizaine. Sans ce zéro symbolisant l’absence de cet ordre de grandeur dans « 1 104 », le nombre ne pourrait pas être représenté sans ambiguïté (sans le zéro, s’agit-il de « 1 104 » ou de « 114 » ?). L’absence de zéro réduit la capacité d’un système numéral à maintenir la constance de sa signification à mesure qu’il évolue. L’inclusion du zéro permet aux autres chiffres d’acquérir une nouvelle signification en fonction de leur position par rapport à lui. Ainsi, le zéro nous permet d’effectuer des calculs avec moins d’efforts, qu’il s’agisse de traits de plume dans un grand livre, de pressions du doigt sur une calculatrice ou de gymnastique mentale. Le zéro est le symbole du vide, qui peut être une qualité très utile, comme l’a dit Lao Tseu :
« Nous façonnons l’argile pour en faire un pot, mais c’est le vide à l’intérieur qui contient tout ce que nous voulons. »
Plus philosophiquement, le zéro est emblématique du vide, tel que le décrit Aczel :
«…le vide est partout et il se déplace ; il peut représenter une vérité lorsque vous écrivez un nombre d’une certaine manière – pas de dizaines, par exemple – et un autre type de vérité dans un autre cas, par exemple lorsque vous n’avez pas de milliers dans un nombre !»
On peut établir des analogies avec les fonctions de la monnaie : le zéro est la « réserve de valeur » sur laquelle les chiffres d’ordre de grandeur supérieur peuvent s’échelonner ; c’est la raison pour laquelle nous préférons toujours voir un autre zéro à la fin de notre compte en banque ou de notre solde en bitcoins. De même qu’une réserve de valeur économique saine conduit à une augmentation de l’épargne, qui sous-tend l’investissement et les gains de productivité, une réserve de valeur mathématique saine nous donne un système numérique capable de contenir plus de sens dans moins d’espace et d’effectuer des calculs en moins de temps : deux facteurs qui favorisent également la croissance de la productivité. Là où la monnaie est le moyen par lequel le capital transite continuellement en direction des lieux d’utilisation économique optimale, le zéro donne aux autres chiffres la possibilité d’être utilisés à plusieurs reprises, avec des significations différentes, à des fins différentes.
La deuxième fonction du zéro est d’être un nombre à part entière : c’est le point médian entre tout nombre positif et son équivalent négatif (comme +2 et -2). Avant l’apparition du concept de zéro, les nombres négatifs n’étaient pas utilisés, car la notion de « rien » en tant que nombre n’existait pas, encore moins l’idée du « moins que rien ». Brahmagupta a inversé la ligne des nombres positifs pour créer des nombres négatifs et a placé le zéro au centre, complétant ainsi le système numérique que nous utilisons aujourd’hui. Bien que les nombres négatifs aient fait l’objet d’écrits antérieurs, notamment sous la dynastie Han en Chine (de 206 à 220 avant notre ère), leur utilisation n’a pas été officialisée avant Brahmagupta, car ils fallait que le concept de zéro soit correctement défini et aligné. D’un point de vue visuel, les nombres négatifs sont comme le reflet des nombres positifs projetés à travers le zéro :

Tout comme la monnaie, qui est au cœur de tout système économique, le zéro est le centre de gravité de tout notre système de numération.
Il est intéressant de noter que les nombres négatifs étaient à l’origine utilisés pour signifier les dettes, bien avant l’invention de la comptabilité en partie double, laquelle a opté pour les débits et les crédits (en partie pour éviter l’utilisation de nombres négatifs). Ainsi, le zéro est le « moyen d’échange » entre les domaines positif et négatif des nombres – il n’est possible d’entrer ou de sortir de l’un ou l’autre de ces territoires qu’en passant par le zéro. En allant sous zéro et en conceptualisant les nombres négatifs, de nombreuses constructions mathématiques nouvelles et inhabituelles (mais extrêmement utiles) voient le jour, notamment les nombres imaginaires, les nombres complexes, les fractales et les équations astrophysiques avancées. Tout comme la monnaie, ce moyen d’échange économique, amène une accélération du commerce et de l’innovation, zéro, ce moyen d’échange mathématique, améliore l’échange d’informations et stimule le développement des avancées civilisationnelles qui en découlent :
L’ensemble de Mandlebrot : l’un des exemples de fractale les plus célèbres, une structure mathématique étonnante formée de nombres complexes qui modélise la géométrie de la nature et sa complexité intrinsèque. L’un des exemples les plus connus de beauté mathématique, cette fractale présente une profondeur et une largeur infinies, ainsi qu’une autosimilarité non-répétitive. Le zéro est une condition préalable à une telle modélisation fractale.
La troisième fonction du zéro est de faciliter le calcul de fractions ou de rapports. Par exemple, les Égyptiens de l’Antiquité, dont le système de numération ne comportait pas de zéro, avaient une façon extrêmement laborieuse de traiter les fractions : au lieu de considérer les 3/4 comme un rapport de trois à quatre (comme nous le faisons aujourd’hui), ils les considéraient comme la somme de 1/2 et 1/4. La grande majorité des fractions égyptiennes s’écrivaient sous la forme d’une somme de nombres comme 1/n, où n est le nombre à compter. Sans le zéro, de longues chaînes de fractions unitaires étaient nécessaires pour traiter des rapports plus importants et plus compliqués (beaucoup d’entre nous se souviennent de la pénibilité de la conversion des fractions à l’école). Avec le zéro, nous pouvons facilement convertir les fractions sous forme décimale (comme 1/2 en 0,5), ce qui supprime la nécessité d’effectuer des conversions compliquées lorsqu’il s’agit de fractions. C’est la fonction « unité de compte » du zéro. Les prix exprimés en monnaie ne sont que des rapports d’échange convertis en décimales de prix libellées en monnaie : au lieu de dire « cette maison coûte onze voitures », nous disons « cette maison coûte 440 000 dollars », ce qui correspond au prix de onze voitures de 40 000 dollars. L’argent nous permet de mieux gérer les rapports de change, de la même manière que le zéro nous permet de mieux gérer les rapports numériques.
Les chiffres constituent le niveau ultime d’abstraction objective : par exemple, le chiffre 3 représente l’idée de « trio » ou de « trinité» – une qualité qui peut être attribuée à tout ce qui se présente sous la forme d’un groupe de trois dans l’univers. De même, le chiffre 9 représente la qualité, l’état du « neuf » partagé par tout ce qui est composé de neuf parties. Les chiffres et les mathématiques ont grandement favorisé l’échange interpersonnel de connaissances (qui peuvent être incarnées par des biens ou des services), car les gens peuvent communiquer sur presque tout dans le langage commun du calcul. La monnaie n’est donc que la mesure mathématisée du capital disponible sur le marché : c’est le plus petit dénominateur commun de tous les biens économiques et c’est nécessairement l’actif le plus liquide dont l’offre est la moins sujette à changement. Elle est utilisés comme système de mesure pour les valorisations constamment changeantes du capital (c’est la raison pour laquelle l’or est devenu la monnaie – c’est le métal monétaire dont l’offre est la plus difficile à modifier). Les rapports entre la monnaie et le capital (en d’autres termes : les prix) sont parmi les plus importants au monde, et les rapports sont un élément fondamental de l’être :
« Au commencement était le rapport, et le rapport était avec Dieu, et le rapport était Dieu. » – Jean 1:1*
*(Traduction plus « rationnelle » de l’évangile selon St Jean, le disciple bien-aimé de Jésus: le mot grec pour ratio était λόγος (logos), qui est aussi le terme pour verbe/parole).
La capacité à manipuler les ratios plus efficacement a directement participé au développement de la rationalité chez l’homme, ce mode de pensée basé sur la logique à l’origine de grands mouvements sociaux tels que la Renaissance, la Réforme et le Siècle des Lumières. Pour bien comprendre l’étrange logique du zéro, il faut partir de son point d’origine, la philosophie qui l’a vu naître.
Philosophie du zéro
« Au premier âge des divinités, l’existence naquit de la non-existence. »
– Le Rig Veda
Le zéro est né de l’étrange logique de l’Orient ancien. Il est intéressant de noter que le Bouddha lui-même était un mathématicien reconnu – les premiers livres le concernant, comme le Lalita Vistara, le disent excellent en calcul (une compétence qu’il utilise pour courtiser une certaine princesse). Dans le bouddhisme, le caractère logique du monde phénoménologique est plus complexe que le vrai ou le faux :
« Tout est soit vrai,
soit faux,
ou à la fois vrai et faux,
ou ni vrai ni faux.
Tel est l’enseignement du Seigneur Bouddha ».
C’est le Tétralemme (ou les quatre coins du Catuṣkoṭi, N.d.T. les quatre valeurs de vérité possibles pour une proposition) : la clé pour comprendre l’apparente étrangeté de cette ancienne logique orientale est le concept de Shunya, un mot hindi qui signifie zéro : il est dérivé du concept philosophique bouddhiste de Śūnyatā (ou Shunyata). Le but ultime de la méditation est d’atteindre l’éveil, ou un état idéal de nirvana, qui revient à se vider complètement de toute pensée, de tout désir et de tout attachement au monde. La réalisation de ce vide absolu est l’état d’être dans le Shunyata : un concept philosophique intimement lié au vide, comme le décrit l’écrivain bouddhiste Thich Nhat Hanh :
« La première porte de la libération est la vacuité, Shunyata
La vacuité signifie toujours être vide de quelque chose
La vacuité est la Voie du Milieu entre l’existant et le non-existant.
La réalité dépasse les notions d’être et de non-être.
La véritable vacuité est appelée « être merveilleux », parce qu’elle va au-delà de l’existence et de la non-existence.
La concentration sur la vacuité est un moyen de rester en contact avec la vie telle qu’elle est, mais il faut la pratiquer et ne pas se contenter d’en parler ».
L’expérience méditative du vide est encore décrite par un moine bouddhiste de l’ancien temple de Wats, en Asie du Sud-Est :
« Lorsque nous méditons, nous comptons. Nous fermons les yeux et nous ne sommes conscients que de l’endroit où nous nous trouvons dans le moment présent, et de rien d’autre. Nous comptons l’inspiration, 1, et l’expiration, 2, et nous continuons ainsi. Lorsque nous arrêtons de compter, c’est le vide, le chiffre zéro, la vacuité ».
La méditation permet de faire l’expérience directe du vide. Dans un véritable état méditatif, le Shunyata et le chiffre zéro ne font qu’un. Le vide est le conduit entre l’existence et la non-existence, tout comme le zéro est la porte entre les nombres positifs et négatifs : chacun étant le reflet parfait de l’autre. Le zéro a vu le jour dans l’Orient ancien, incarnant le concept profondément philosophique et expérimental de vide absolu. Empiriquement, nous savons désormais que la méditation est bénéfique pour le cerveau à bien des égards. Il semble également que sa contribution à la découverte du zéro ait aidé à forger une idée qui profiterait à jamais à l’intelligence de l’humanité – une sorte de mise à jour logicielle de notre esprit collectif.
Bien que sa découverte provienne d’un état spirituel, le zéro est un concept profondément pratique : la meilleure façon de le comprendre est sans doute de le considérer comme un produit de la fusion de la philosophie et du pragmatisme. En traversant zéro pour entrer dans le territoire des nombres négatifs, nous rencontrons les nombres imaginaires, dont l’unité de base est la racine carrée de -1, que l’on désigne par la lettre i. Le nombre i est paradoxal : considérez l’équation ±x² + 1 = 0 ; les seules réponses possibles sont la racine carrée positive de -1 (i) et la racine carrée négative de -1 (-i ou i³). Si l’on passe à une dimension supérieure, l’équation ±x³ + 1 = 0 donne comme réponses possibles +1 ou -1. Ces réponses continuent d’alterner entre les domaines réel et imaginaire au fur et à mesure que leurs formules sous-jacentes s’exponentialisent. En les visualisant dans les domaines réel et imaginaire, nous trouvons un axe de rotation centré sur zéro avec des orientations qui rappellent le tétralemme : un vrai (1), un faux (i), un à la fois vrai et faux (-1 ou i²), et un ni vrai ni faux (-i ou i³) :
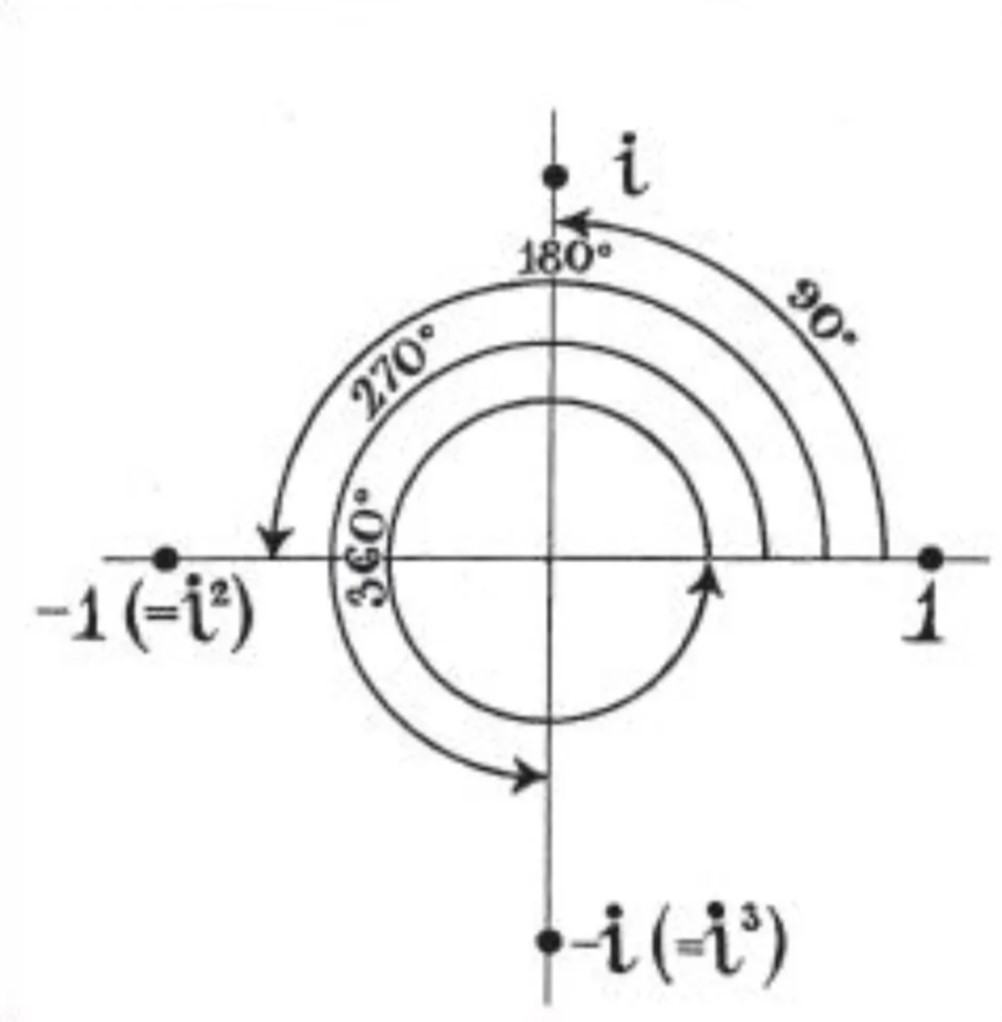
Le zéro est le point d’appui entre les plans des nombres réels et imaginaires.
Le passage du zéro au royaume des nombres négatifs et imaginaires offre une forme de logique plus continue que la logique discrète du « ou bien, ou bien », communément attribuée à Aristote et ses disciples. On a là un cadre moins « noir et blanc » que le système logique binaire d’Aristote, basé sur le vrai ou le faux, et on a accès à de nombreux niveaux de logique ; une carte plus précise des nombreuses « nuances de gris » que l’on trouve dans la nature. La logique de continuité s’insinue partout dans le monde: par exemple, quelqu’un va dire « elle n’était pas inintéressante » ce qui signifie que l’intérêt qu’elle suscitait était ambivalent, quelque part entre intéressant et inintéressant. Cette perspective est souvent plus réaliste qu’une évaluation binaire de l’intérêt ou de l’absence d’intérêt.
Il est important de noter que le zéro nous a apporté le concept d’infini, remarquablement absent de l’esprit des logiciens grecs de l’Antiquité. Les rotations autour de zéro à travers les axes des nombres réels et imaginaires peuvent être mathématiquement mises à l’échelle dans un modèle tridimensionnel appelé la sphère de Riemann. Dans cette structure, le zéro et l’infini sont des reflets géométriques l’un de l’autre et peuvent se transposer en un éclair de permutation mathématique. Toujours au pôle opposé de cette interprétation mathématique tridimensionnelle du tétralemme, nous trouvons le jumeau du zéro, l’infini.

En passant du plan des nombres réels et imaginaires à la troisième dimension, nous découvrons le jumeau du zéro : l’infini.
Les polarités jumelles du zéro et de l’infini s’apparentent au yin et au yang, comme le décrit Charles Seife, auteur de Zéro : La biographie d’une idée dangereuse :
« Le zéro et l’infini se sont toujours ressemblés de manière suspecte. Multipliez zéro par n’importe quoi et vous obtenez zéro. Multipliez l’infini par n’importe quoi et vous obtenez l’infini. En divisant un nombre par zéro, on obtient l’infini ; en divisant un nombre par l’infini, on obtient zéro. L’ajout de zéro à un nombre le laisse inchangé. L’ajout d’un nombre à l’infini laisse l’infini inchangé. »
Dans la philosophie orientale, la parenté du zéro et de l’infini était logique : ce n’est que dans un état de néant absolu que les possibilités deviennent infinies. La logique bouddhiste soutient que tout est entrelacé en permanence : un vaste réseau causal dans lequel tout est inexorablement lié, de sorte qu’aucune chose ne puisse vraiment être considérée comme indépendante – comme ayant sa propre essence isolée et non interdépendante. Dans cette optique, l’interrelation est la seule source de justification. Fondamentale dans leur enseignement, cette vérité est ce que les bouddhistes appellent le principe d’origine interdépendante, c’est-à-dire que toutes les choses dépendent les unes des autres. La seule exception à cette vérité est le nirvana : la libération des cycles sans fin de la réincarnation. Dans le bouddhisme, le seul chemin vers le nirvana passe par la vacuité pure :

Le nirvana, le but spirituel ultime du bouddhisme, est atteint en pénétrant dans le vide par la méditation – c’est là que le zéro a été découvert.
D’anciens textes bouddhistes affirment que « le véritable absolu et la véritable liberté doivent être le néant ». De ce point de vue, l’invention du zéro est unique ; elle peut être considérée comme la découverte du néant absolu, une qualité latente de la réalité qui n’était pas présupposée jusqu’alors dans la philosophie ou les systèmes de connaissance comme les mathématiques. Sa découverte s’est révélée être une force émancipatrice pour l’humanité, dans la mesure où le zéro est à la base de la réalité mathématisée et logicielle que nous connaissons aujourd’hui.
Le zéro fut une libération découverte au plus profond de la méditation, un vestige de vérité déniché tout près du nirvana – ce lieu où l’on rencontre une conscience universelle, illimitée, infinie : Le royaume de Dieu en nous. Pour les bouddhistes, le zéro était un murmure de l’univers, du dharma, de Dieu (les mots nous font toujours défaut dans le domaine du divin). Paradoxalement, le zéro allait faire voler en éclats l’institution qui avait bâti sa structure de pouvoir en monopolisant l’accès à Dieu. En prenant pied dans le vide, l’humanité fit la découverte du substrat le plus profond et le plus solide sur lequel fonder la société moderne : le chiffre zéro s’avéra être un élément absolument essentiel de l’infrastructure qui permit l’interconnexion du monde par les réseaux de télécommunication, et qui inaugura l’étalon-or et l’ère numérique (les deux principaux inducteurs de Bitcoin) de nombreuses années plus tard.
Ouvrir une voie vers l’avenir : les concepts jumeaux de l’infini et du zéro allaient déclencher la Renaissance, la Réforme et le Siècle des Lumières – autant de mouvements qui ont érodé le pouvoir de l’Église catholique, alors institution dominante dans le monde, et préparé le terrain pour l’État-nation industrialisé.






